The energy of a photon with wavelength
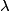 is is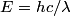 where  is the speed of light and is the speed of light and 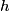 is Planck's constant. If we assume the energy released in the femtosecond pulse is equal to the peak power multiplied by one femtosecond, then the number of photons released is is Planck's constant. If we assume the energy released in the femtosecond pulse is equal to the peak power multiplied by one femtosecond, then the number of photons released is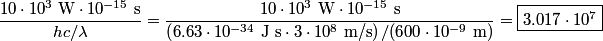 Therefore, answer (B) is the correct answer. |